Przyszedł w końcu dzień, w którym udało mi się reaktywować cykl wpisów o opcjach. Od pierwszego wpisu (Kowalski, opcje!) minęło już prawie 8 miesięcy. Prawdę mówiąc, spodziewałem się wówczas, że znacznie szybciej pójdzie mi publikowanie kolejnych postów. Pierwotnie zakładałem ukończenie części o zdefiniowanym ryzyku jeszcze w tym roku. Aktualnie będzie to raczej niemożliwym do wykonania, choć postaram się dołożyć wszelkich starań, aby do końca roku pojawiło się jak najwięcej nowych wpisów. Pierwszym krokiem w tym kierunku będzie dzisiejszy post. Post, w którym wejdziemy w świat współczynników greckich. Od tej pory, będą nam one towarzyszyły za każdym razem, kiedy zdecydujemy się na handel opcjami. Na pierwszy ogień pójdzie delta, jednak zanim przejdziemy do samego sedna dzisiejszego wpisu, chciałbym omówić dwie kwestie. Zatem do rzeczy.
Iron condor – podsumowanie
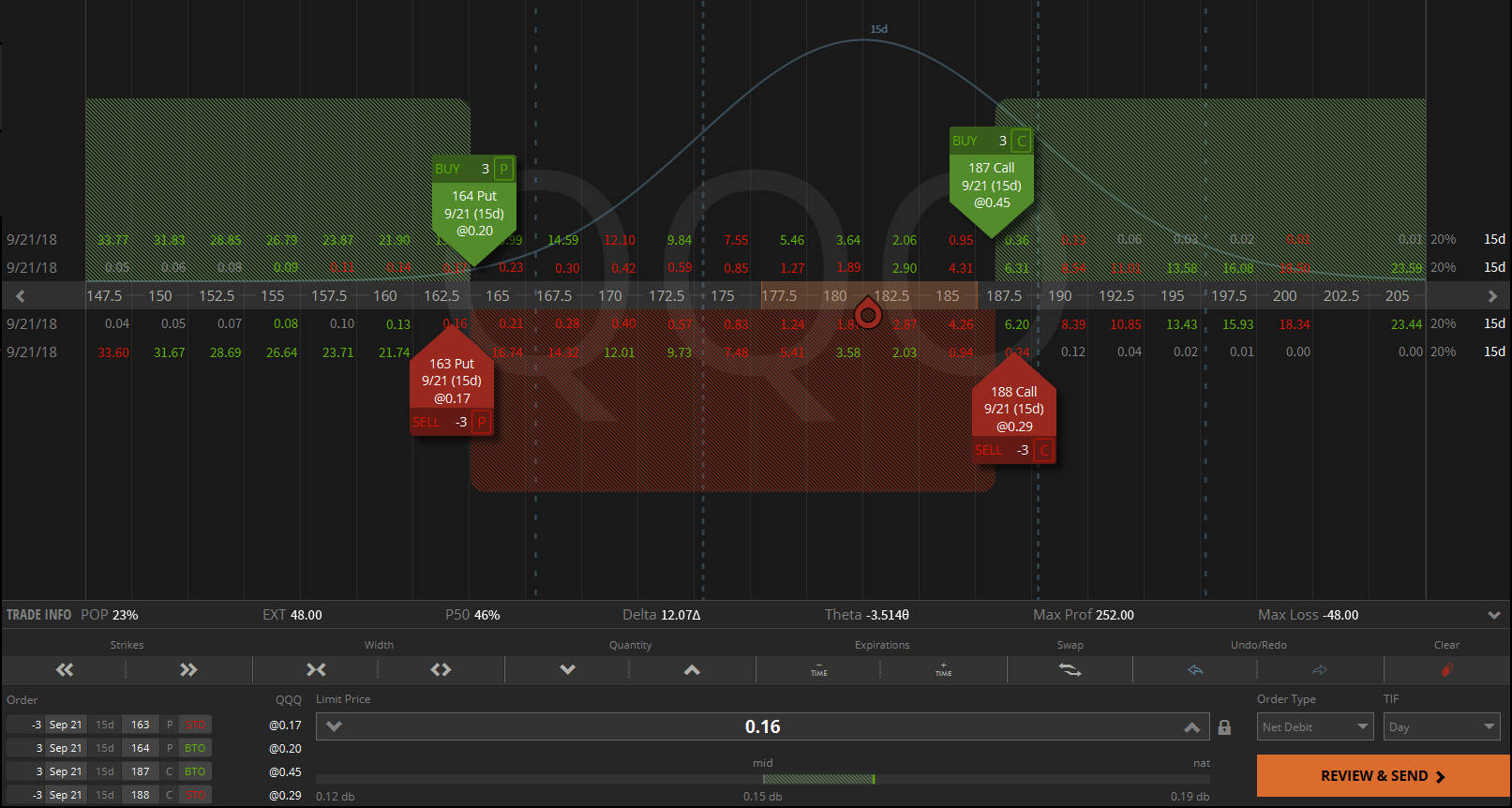
W pierwszej kolejności chciałbym podsumować pozycję jaka została zawarta przy okazji publikacji poprzedniego wpisu. Podobnie jak miało to miejsce w przypadku przykładu ze spreadem, tak i tym razem pozycji daleko było do miana idealnej. Nie taki był jednak ówczesny zamysł. Kluczem było bowiem wykorzystanie wszystkich nowych informacji. Mając to na uwadze, udało mi się poskładać taką oto pozycję na QQQ:
Tym razem miałem zdecydowanie więcej szczęścia niż we wspomnianym wyżej przypadku ze spreadem. Udało mi się bowiem zająć pozycje po cenie lepszej niż średnia. I to pomimo faktu, zajmowania pozycji w 3 kontraktach. Koniec końców, udało mi się zebrać 96 dolarów. Celem, zgodnie z przytoczonymi wówczas założeniami, było zarobienie na tej pozycji przynajmniej połowy tej wartości. Taki też cel udało mi się osiągnąć – pozycję bowiem odkupiłem dokładnie za 16 centów – co daje nam w sumie 48 dolarów. Poniżej screen z dnia, w którym pozycja została zamknięta:
To tyle, jeżeli chodzi o podsumowanie pierwszego w naszej karierze, żelaznego kondora. Pora więc przejść do sedna dzisiejszego wpisu.
Czym jest model wyceny opcji?
Aby w pełni zrozumieć to, czym są współczynniki greckie, niezbędne jest poruszenie tematu modelu wyceny opcji. Oczywiście nie będę się tutaj zagłębiał w nikomu niepotrzebne szczegóły. Warto jednak poznać ogólny zarys, dzięki czemu będziemy świadomi faktu, że nic tutaj nie bierze się z powietrza. Wszytko o czym będziemy mówili przy okazji cyklu o opcjach, ma swoje matematyczne uzasadnienie i wywodzić się będzie z tego właśnie modelu. To właśnie w oparciu o model wyceny opcji (OPM – Option Pricing Model), wyprowadzone zostały jego pochodne, znane jako współczynniki greckie.
Aktualnie wykorzystywanym modelem wyceny opcji, jest ten przedstawiony przez Fishera Blacka i Myrona Scholesa w 1973 roku. Swój udział w tworzeniu tego modelu miał również Robert C. Merton, stąd czasami możemy spotkać się z nazwą Modelu Blacka-Scholesa-Mertona. Zdecydowanie bardziej powszechną nazwą, jest jednak Model Blacka-Scholesa. Nie zagłębiając się we wszystkie niuanse, wzory na wycenę opcji CALL oraz PUT wyglądają następująco:
Do tego należy dodać kolejne wzory, które prezentują się w następujący sposób:
Oczywiście, nikt nie będzie wymagał od Was znania tych wzorów. Z puntu widzenia tradera, nmało istotne są również poczynione przez Blacka i Scholesa założenia do powyższego modelu. Jednak, jak już wspomniałem, warto jest być świadomym, że wszystko znajduje swój początek właśnie tutaj. Wycena opcji zgodna z modelem to jedna kwestia. Rynek zawsze weryfikuje tego rodzaju teoretyczne rozważania. Warto jest jednak mieć na względzie fakt, że niektóre platformy udostępniają nam wgląd do teoretycznej wyceny danej opcji, w oparciu o powyższy model. Czasami okazuje się to być przydatnym narzędziem, szczególnie w sytuacji gdy rynek znacząco odbiega o wyceny teoretycznej. Warto jest wtedy dokładnie przemyśleć zajmowanie takiej pozycji. Platforma tastyworks również daje nam taką możliwość:
Delta – wprowadzenie
Udało nam się zbudować solidne fundamenty pod kolejne wpisy, pora więc na przejście do meritum. Czym tak na prawdę jest delta? Oprócz tego, że jest to pierwsza z grek jakim przyjrzymy się naszym cyklu. Delta jest jednym z najbardziej wszechstronnych współczynników greckich, które przyjdzie nam omawiać. Głównie ze względu na fakt, że posiada ona szereg zastosowań. Jest to o tyle istotne, że będziemy się nimi posługiwali niezwykle często. Zanim jednak przejdziemy do sedna, chciałbym przytoczyć odrobinę teorii na jej temat. Zacznijmy zatem od definicji oraz wzorów na deltę:
Za wikipedią:
Współczynnik delta oznacza przewidywany stopień zmiany ceny opcji w zależności od małej zmiany ceny instrumentu bazowego będącego przedmiotem opcji.
To tyle jeżeli chodzi o teorię. Pytanie powinno teraz brzmieć: co tak na prawdę to oznacza? W dużym przybliżeniu, możemy powiedzieć, że delta opisuje nam związek pomiędzy ceną instrumentu bazowego, a ceną wykonania danej opcji. Jest to oczywiście duże uproszczenie, jednak w dużej mierze oddaje ono kluczowe znaczenie tej pochodnej.
W przypadku instrumentu bazowego, jakim mogą być tutaj akcje, sprawa jest prosta. Każdy zmiana ceny o 1 dolara, powoduje identyczną zmianę wartości naszej pozycji. Akcje spółki Apple idą w górę o 20 dolarów, nasza pozycja rośnie o 20 dolarów na każdą zakupioną akcję. Logiczne. W przypadku opcji sprawa wygląda inaczej. Zmiana ceny instrumentu bazowego, nie spowoduje identycznej zmiany wartości naszej pozycji w opcjach na dany instrument (ceteris paribus). Delta pomaga nam estymować zmianę wyceny naszej pozycji w przypadku zmiany ceny instrumentu bazowego (ceteris paribus). Innymi słowy. Przy zmianie ceny instrumentu bazowego, nasza pozycja w opcji wystawionej na ten instrument, złapie jedynie część tego ruchu. Delta pomaga nam określić jak duża to będzie część. Jest to pierwsza z trzech właściwości delty.
Delta i jej znaczenie w codziennym handlu
Jak już zdążyłem wcześniej wspomnieć, delta jest jednym z najbardziej wszechstronnych współczynników greckich. Co więcej, praktycznie niemożliwym jest jej całkowite wykluczenie z procesu decyzyjnego przy zajmowaniu pozycji. Do tej pory sztuka ta nam się udawała, jednak wówczas nasza uwaga skupiona była na inne aspekty. Ze względu na swoje właściwości, delta będzie nam teraz towarzyszyła na każdym kroku. Jest to absolutnie kluczy współczynnik, z którym musimy się zapoznać chcąc stawiać kolejne kroki w świecie opcyjnym. Inna rzeczą, na która zdążyłem już zwrócić uwagę to fakt, że delta posiada kilka znaczeń, właściwości. To właśnie tym znaczeniom przyjrzymy się w kolejnych akapitach. Pierwszym z nich, będzie przytoczona wcześniej zależność pomiędzy ceną instrumentu bazowego, a ceną danej opcji.
Miara zasięgu ruchu
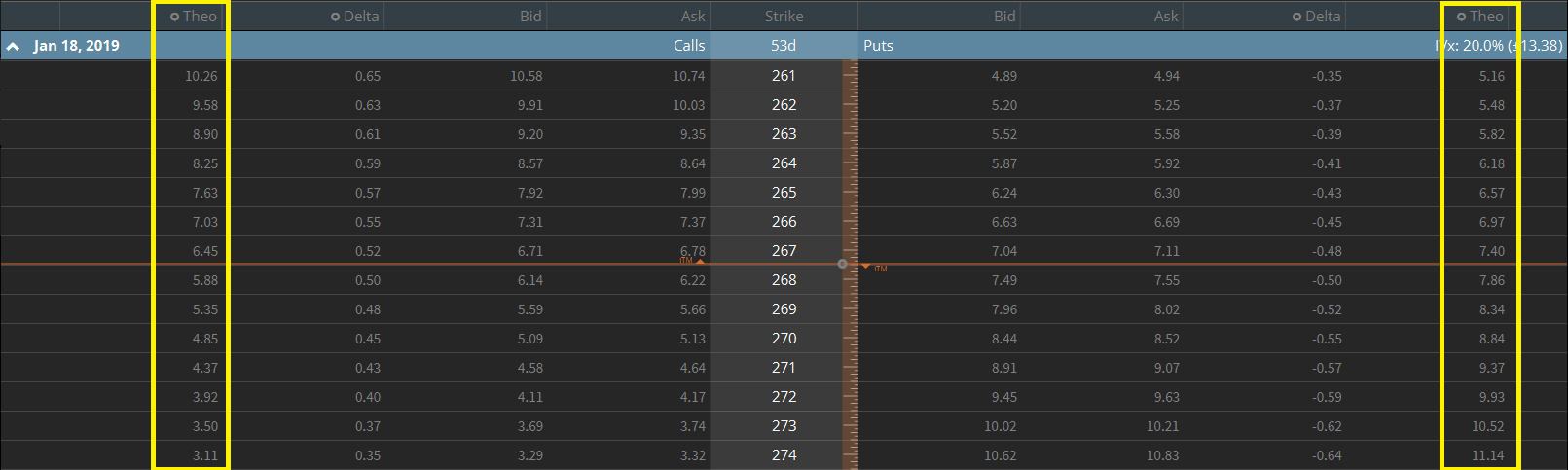
Wiemy już, że opcje wyłapują jedynie część z ruchu jaki obserwować możemy na instrumencie bazowym. Delta pomaga nam określić, jak duża jest to część. Dla przykładu weźmy opcje na SPY:
Widzimy, że delta opcji CALL z ceną wykonania 267 wynosi 0.51. Co to oznacza w naszym przypadku? Znaczy to ni mniej, ni więcej tyle, że w przypadku wzrostu ceny o 1 dolara, wycena naszej opcji wzrośnie o 0,51 dolara, tj. 51 centów (ceteris paribus). Oczywiście jest to wartość, która obowiązuje w danym momencie. Wpływa na nią ma szereg różnych czynników, z czego najistotniejszym jest oczywiście cena instrumentu bazowego. Wraz z jej zmianą, delta opcji z ceną wykonania 267 będzie ulegała zmianom. Oczywiście nie jest to jedyny czynnik, który będzie miał wpływ na wartość naszej delty. Wystarczy bowiem rzucić okiem na wzór, jakim posługujemy się do jej wyznaczenia, aby zdać sobie sprawę z istnienia innych zmiennych.
Warto jest w tym momencie zaznaczyć, że wartość, która podawana jest nam przez platformę, to wartość delty dla jednej opcji. Jak dobrze pamiętamy z jednego z poprzednich wpisów, każdy kontrakt opiewa na 100 jednostek instrumentu bazowego. Z tego też powodu, zawsze należy pomnożyć powyższą wartość przez 100. W takim wypadku, pozycja w jednym kontrakcie opcyjnym na SPY, z ceną wykonania 267, będzie charakteryzowała się deltą na poziomie 51. Jest to o tyle istotne, że pomaga nam to określić faktyczny wpływ zmiany ceny instrumentu bazowego na nasz portfel. Dodatkowo, rozmawiając z innymi traderami, padały będą wartości dla pełnych kontraktów. Nikt raczej nie powie, że zajął pozycję z deltą 0.51.
Zakres delty
Jak zatem widzimy, delta określa procentową cześć zmiany ceny instrumentu bazowego, którą zostanie obciążona wycena naszej opcji (przy innych czynnikach pozostających bez zmian). Gdyby w naszym przykładzie doszło do zmiany ceny instrumentu bazowego o 2 dolary, wycena opcji zmieniłaby się o 1,02 dolara (51% z 2 dolarów). W przypadku zmiany ceny o 70 centów, nasza pozycja zmieniłaby się o 36 centów. Mając to na uwadze, logicznym wydaje się być fakt, że delta nie może przyjmować wartości większych niż 1. Dlaczego? Nie jest bowiem możliwe złapanie większej części, niż całości ruchu na instrumencie bazowym. Z tego też względu zakres delty, dla danej opcji mieści się przedziale od -1 do 1. Skąd wartość ujemna? O tym w kolejnym akapicie.
Zanim do tego przejdziemy, chciałbym zwrócić uwagę na jedną, niezwykle istotną rzecz. Biorąc pod uwagę fakt, ze kontrakt opiewa na 100 jednostek instrumentu bazowego, wartości delty dla pojedynczego kontraktu mieściły się będą w przedziale od -100 do 100. Pamiętajmy jednak, że odnosi się to tylko i wyłącznie do jednego kontraktu! Zajmując pozycję w dwóch kontraktach, granice zasięgu rozrosną się do -200 i 200. Dla trzech, do -300 i 300. W naszym przykładzie, zajmując pozycję w trzech kontraktach, delta przyjmie wartość 153 (dodatnią lub ujemną).
Kierunek pozycji
Delta pozwala nam również w bardzo szybki sposób określić kierunek naszej pozycji. Może nie jest to tak istotny czynnik w momencie zawierania pozycji, jednak zarządzając portfelem złożonym z kilku/kilkunastu pozycji, znacząco ułatwia nam to odpowiednią kontrolę. Patrząc na wcześniejszy screen z platformy, możemy zauważyć, że delta dla opcji CALL przyjmuje wartości dodatnie, natomiast delta dla opcji PUT – ujemne. Dlaczego tak się dzieje? Z prostego powodu. Zajmując pozycje długą (czy to w pojedynczej opcji, czy też strategii opcyjnej) delta zawsze będzie przyjmowała wartości dodatnie. W przypadku pozycji krótkiej, będą to wartości ujemne. Platforma pokazuje nam zatem wartości delty z perspektywy kupującego. Warto jest tutaj odświeżyć sobie informacje zawarte w jednym z poprzednich wpisów, gdyż będą one tutaj kluczowe.
Mając na uwadze powyższe, logicznym wydaje się być fakt, że zajmując krótką pozycję w opcji CALL z ceną wykonania 267, delta przyjmie wartość ujemną (dokładnie -0.51, czyli -51). Oznacza to również tyle, że w przypadku wzrostu ceny instrumentu bazowego o 1 dolara, wartość opcji wzrośnie o 51 centów (ceteris paribus), a co za tym idzie, nasza pozycja będzie wykazywała stratę w wysokości 51 dolarów (51 centów na jedną akcję – kontrakt opiewa na 100 jednostek). Zrozumienie tej zależności jest absolutnie kluczowe i warto jest poświęcić odrobinę czasu na jej opanowanie.
Delta naszej pozycji w strategii opcyjnej będzie zatem sumą wszystkich delt z poszczególnych opcji wykorzystanych do jej zbudowania. Analogicznie dla naszego portfolio, będzie to suma delt wszystkich pozycji w naszym portfelu. Warto jest tutaj rzucić okiem na omawianą w poprzednim wpisie strategię Iron Condor. Jest to strategia o neutralnym nastawieniu, dlatego też delta powinna oscylować w okolicach zera. Czy faktycznie tak jest? Spójrzmy na poniższy przykład:
Delta na poziomie -0.27 (dla całego kontraktu). Można zatem założyć, że jest to pozycja neutralna.
Prawdopodobieństwo wypracowania zysku
Ostatnim z zastosowań delty, jest oszacowanie przybliżonego prawdopodobieństwa wypracowania zysku na danej pozycji. Mówimy tutaj oczywiście tylko i wyłącznie o jednej opcji. Zasada ta nie znajduje zastosowania w przypadku złożonych strategii opcyjnych, czy też w odniesieniu do całego portfela. Co więcej, jest to tylko przybliżony szacunek. Nie zmienia to jednak faktu, że czasami informacja ta okazuje się być przydatną. Jak dokładnie możemy z tego skorzystać?
Sprawa jest prosta. Delta określa nam bowiem przybliżony szacunek prawdopodobieństwa, że dana opcja wygaśnie ITM. Co to oznacza? W pierwszej kolejności, warto sobie przypomnieć co oznacza skrót ITM. Pisałem o tym w jednym z poprzednich wpisów. Mając tę wiedzę, wiemy już w jaki sposób możemy ją wykorzystać. Wygaśnięcie opcji ITM jest oczywiście korzystne dla jej nabywcy. Z tego też powodu, przytaczany wcześniej przykład z ceną wykonania 267 i deltą na poziomie 0.51, pozwala jej nabywcy określić przybliżone prawdopodobieństwo wypracowania zysku. Istnieje bowiem 51% szans na to, że opcja przebije cenę wykonania i zostanie zamknięta będąc ITM. Oczywiście samo przebicie ceny wykonania nie wystarczy do tego, aby wypracować zysk. Wzrost ceny musi bowiem dodatkowo pokryć koszta poniesione na nabycie takiej opcji. Warto jest mieć ten fakt zawsze na uwadze.
Analogicznie, zajmując pozycję krótka w przykładowej opcji, mamy 49% szans na to, że nasza pozycja przyniesie nam zysk. Nietrudno się zatem domyśleć, że im wyższa wartość delty, tym więcej przyjdzie nam zapłacić za taką opcję.
Delta – podsumowanie
To tyle, jeżeli chodzi o dzisiejszy wpis. Bez wątpienia warto jest poświęcić odrobinę czasu na to, aby w pełni zrozumieć poruszone w nim kwestie. Zdecydowanie ułatwi nam to poruszanie się w świecie opcyjnym. Oczywiście nie ma jednoznacznej odpowiedzi na pytanie, w jaką wartość delty powinniśmy celować zajmując nasze pozycje. Wszystko zależy od kontekstu, jak również ryzyka jakie chcemy ponieść decydując się na dane zagranie. Wydaje mi się, że kwestia ta powinna być przez wszystkich w pełni zrozumiała.
Na koniec chciałbym również zaznaczyć, że musimy sobie zdawać sprawę z faktu, że delta (oraz wszystkie współczynniki greckie) jest wartością dynamiczną. Greki zmieniają się wraz ze zmianą wszystkich czynników, które mają na nie wpływ. To, że delta naszej pozycji w momencie jej zawarcia wynosi przykładowo 51, wcale nie oznacza, że pozostanie ona na tym poziomie aż do jej wygaśnięcia. Delta cały czas będzie ulegała zmianom. Kluczowa będzie zatem jej odpowiednia kontrola. Jednak jest to zagadnienie na jeden z późniejszych wpisów w cyklu.
Pierwotnie zakładałem publikację oddzielnego wpisu dla każdego z współczynników. Możliwe jednak, że plan ten ulegnie zmianie i uda mi się zmieścić kolejne greki w jednym, większym poście. Wszystko zależy jednak od tego, czy uda mi się wszystko zwięźle i w pełni opisać.
Powyższy tekst jest jednym z wpisów cyklu artykułów traktującym o opcjach. Jeżeli jesteś zainteresowany pozostałymi postami zapraszam na stronę: Opcje.


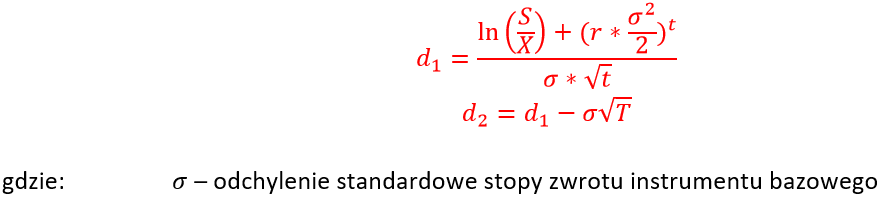



2 thoughts on “Delta i jej trzy oblicza”